Transformer做的千层饼
- Posted on:
- By: CastellanZhang
- With:
Transformer做的千层饼
本文同时发布在我的微信公众号“AI推公式”,和我的知乎专栏(知乎ID:CastellanZhang),欢迎关注。

1. 前言
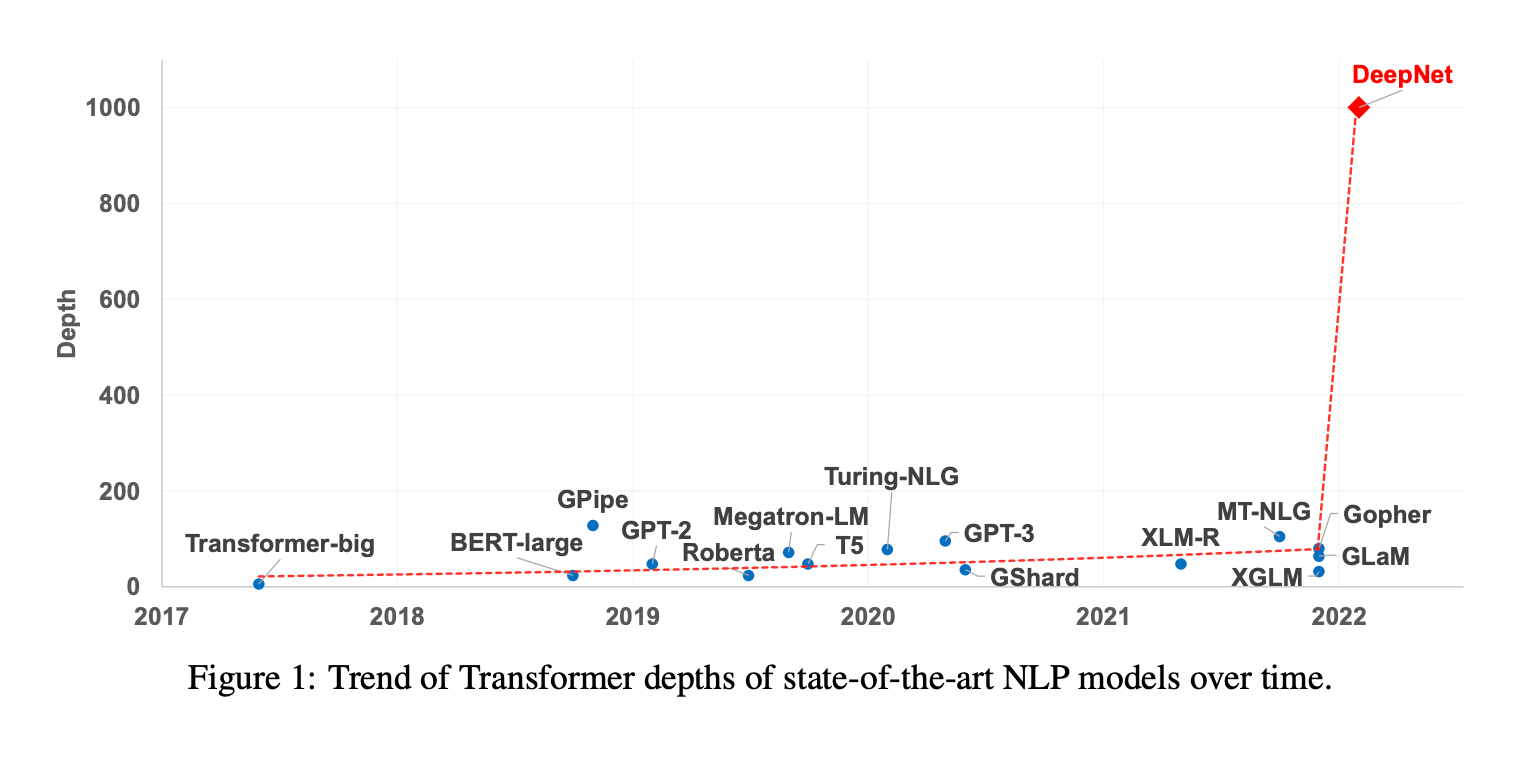
Transformer做的千层饼吃过没?
最近看到一篇微软出的paper[1],把Transformer堆到了1000层,并在一些NLP任务上取得了很好的效果,叹为观止。不是靠暴力调参,而是有分析,有推导,理论结合实践,整个过程值得仔细学习。不过感觉其中的数学推导有些地方值得商榷,我会按照我的理解重新梳理和补充。paper中不仅分析了只有encoder的结构(比如BERT),还分析了包含decoder的结构,分析过程大同小异,因此为了省事,我在本文中只讨论纯encoder的结构。
2. 具体做法
现在的深度模型都在极度膨胀,变得一个比一个大,有的横向发展,有的纵向拉伸,比如很多人都在玩Transformer垒积木,越垒越高,但始终无法突破1000层。这一次微软的大神们终于冲破玄关,一举成功。
论文一开始通过实验分析了前人为何失败,问题不在于大家一般认为的梯度爆炸,而是模型更新爆炸,即参数更新后模型输出的增量幅度 $\Vert \Delta F\Vert $ 的爆炸,模型越深,增量幅度越大,导致训练一开始就很容易陷入糟糕的局部最优,反过来又带来梯度消失问题,更加难以摆脱局部最优。
针对症结所在,对Transformer做了修改,提出DeepNet网络结构。其实改动很小,就是把每个子层中的Post-LN换成了DEEPNORM。代码大概长这个样子:

DEEPNORM数学公式为:
$$\mathbf x_{l+1}=LN(\alpha \mathbf x_l+G_l(\mathbf x_l,\theta_l))$$
其中的 $\alpha$ 为常数,$G_l(\mathbf x_l,\theta_l)$ 是代表第 $l$ 个Transformer的子层(如attention层或FFN层)的函数,$\theta_l$ 为子层的模型参数。公式中看不出来的是,attention层和FFN层中的参数初始化很有讲究,对于attention中的 $W^V$ 和 $W^O$ 、FFN中的 $W^1$ 和 $W^2$,都用nn.init.xavier_normal_(w, gain=β)初始化;而对于attention中的 $W^Q$ 和 $W^K$ ,用 nn.init.xavier_normal_(w, gain=1)初始化。
3. Xavier Normal初始化【补充】
xavier normal初始化为何方神圣?paper里没讲,我来补充一下。
先说具体怎么操作,很简单。假设有 $L$ 层全连接层,激活函数为 $f$ ,第 $l$ 层输入为 $n_l$ 维向量 $\mathbf x_l$,状态值为 $n_{l+1}$ 维向量 $\mathbf y_l$,满足:
$$\mathbf y_l=\mathbf x_lW^l+\mathbf b^l$$
$$\mathbf x_{l+1}=f(\mathbf y_l)$$
那么参数初始化时,$\mathbf b^l$ 置为0,$W^l$ 每个元素 $w_{ij}$ 均采样自正态分布 $N(0,\sigma_l^2)$,方差 $\sigma_l^2=1/n_l$,即输入维度的倒数。
(注:xavier normal初始化一般的标准做法是方差 $\sigma_l^2=2/(n_l+n_{l+1})$,为输入和输出维度均值的倒数。这是同时考虑了前向传播输入输出的方差和后向传播梯度的方差都要基本不变,做的折衷方案。对于这篇paper,主要考虑前向传播,所以我认为不采用这种反而更好。)
这么做有什么用?
假设第 $l$ 层输入 $\mathbf x_l=(x_{l,1},x_{l,2},…,x_{l,n_l})$ 的每一个元素 $x_{l,i}$ 独立同分布,即方差相同,统一记为 $var[x_l]$ ,在某些条件下,xavier初始化可以使得输出的方差 $var[x_{l+1}]$ 基本不变,如果假设输入输出的均值 $E[x_{l}]=E[x_{l+1}]=0$,则相当于 $E[(x_{l+1})^2]$ 和 $E[(x_{l})^2]$ 相比基本不变,这里 $x_{l+1}$ 和 $x_l$ 分别表示向量 $\mathbf x_{l+1}$ 和 $\mathbf x_l$ 中的任一元素,下同。而 $E[\Vert \mathbf x_{l+1}\Vert ^2]=E[\sum_i(x_{l+1,i})^2]=n_{l+1}E[(x_{l+1})^2]\overset{\mathrm\Theta}{=}n_{l+1}E[(x_{l})^2]=n_{l+1}/n_lE[\Vert \mathbf x_{l}\Vert ^2]$ ,即 $\mathbf x_{l+1}$ 和 $\mathbf x_l$ 相比,模长的量级基本不变,只和维度比值的平方根成正比。这里符号 $\overset{\mathrm\Theta}{=}$ 是仿照paper里的写法,表示量级相同。
还可以证明,若将 $W^l$ 初始化正态分布的标准差缩放 $\beta$ 倍,即 $\sigma_l^2=\beta^2/n_l$,则 $E[(x_{l+1})^2]\overset{\mathrm\Theta}{=}\beta^2E[(x_{l})^2]$,假设输入输出的维度相同,则 $\mathbf x_{l+1}$ 和 $\mathbf x_l$ 相比,模长 $\Vert \mathbf x_{l+1}\Vert $ 的量级也缩放了 $\beta$ 倍。这就是代码nn.init.xavier_normal\_(w, gain=β)中的参数 gain=β 的作用。
可能有人已经注意到了,上面的分析都基于输入输出均值为0的假设,但对于ReLU激活函数,根本不成立。没关系,可以证明,稍微修改一下初始化正态分布的方差,让 $\sigma_l^2=2\beta^2/n_l$ 即可,同样可以达到模长缩放 $\beta$ 倍的目的,这正是kaiming初始化的做法。在这篇paper中主要研究量级的变化,对这种常数项的变化都忽略了。
4. 数学原理分析
上面介绍了做法,再来分析这么做为何能将 $\Vert \Delta F\Vert $ 限制住。
先看Attention子层,论文里简化了分析,只研究1-head的情况:
设 $Q,K,V\in\mathbf R^{n\times d}$,且 $W^Q,W^K,W^V\in\mathbf R^{d\times d_k}$,$W^O\in\mathbf R^{d_k\times d}$,则Attention操作可以表示为:
$$
Attn(Q,K,V)=softmax(\displaystyle\frac{QW^Q(KW^K)^T}{\sqrt{d_k}})VW^VW^O
$$
比如对于self-attention,三个参数 $Q,K,V$ 都是输入 $X\in\mathbf R^{n\times d}$,Attn输出维度同样是 $n\times d$。
然后给出一个引理4.1,是为了说明 $W^Q$ 和 $W^K$ 不会影响Attention输出的量级,所以这两项参数初始化无需缩放,gain参数设为1即可。
4.1 引理
给定 $X=(\mathbf x_1,\mathbf x_2,…,\mathbf x_n)^T\in\mathbf R^{n\times d}$, 对于任意 $\mathbf x_i$,$i\in[1,n]$,都有 $var(\mathbf x_i)=1,mean(\mathbf x_i)=0$,且有 $q_i\in\mathbf R$,那么
$$
softmax(q_1,q_2,…,q_n)X\overset{\mathrm\Theta}{=}\mathbf x_i
$$
证明:softmax操作后,$\mathbf x_i$ 的权重为 $s_i=e^{q_i}/\sum_{j=1}^n e^{q_j}$,满足 $\sum_{i=1}^n s_i=1$,因此有
$$
\displaystyle\Vert softmax(q_1,q_2,…,q_n)X\Vert =\Vert \sum_{i=1}^n s_i\mathbf x_i\Vert \le\sum_{i=1}^n s_i\Vert \mathbf x_i\Vert
$$
后面不等号是利用了Jensen不等式。
而 $var(\mathbf x_i)=1,mean(\mathbf x_i)=0$,是说 $\mathbf x_i$ 中的d个元素的方差为1,均值为0,因此有 $\Vert \mathbf x_i\Vert =\sqrt{d}$,这里论文有误,少了根号。因此 $\Vert softmax(q_1,q_2,…,q_n)X\Vert \le\Vert \mathbf x_i\Vert =\sqrt{d}$,即可认为 $softmax(q_1,q_2,…,q_n)X$ 和 $\mathbf x_i$ 量级相等。
从证明中可以看出来,所谓量级相等,就是指向量模长的量级相等。
有了这个引理,我们可以断言 $Attn(Q,K,V)\overset{\mathrm\Theta}{=}VW^VW^O$
严格来讲,上面等式左右都是 $n\times d$ 的矩阵,这里的量级相等,是指左边矩阵每一个行向量的模长都和右边矩阵任意行向量的模长量级相等。
接着paper做了进一步简化,将 $W^V$ 和 $W^O$ 简化成了标量 $v$ 和 $w$,即变成了 $Attn(Q,K,V)\overset{\mathrm\Theta}{=}vwV$。类似做法,FFN层简化成了 $FFN(X)\overset{\mathrm\Theta}{=}vwX$,不过这里的 $v$ 和 $w$ 是FFN的参数,不要和Attention层的搞混了。
这么极致简化的合理性在哪里?后文细说。
定义我们的研究目标 $\Vert \Delta F\Vert =\Vert F(x,\theta^{\ast})-F(x,\theta)\Vert $,然后看看在N层DeepNet(即包含N层Attn和N层FFN)下,$\Vert \Delta F\Vert $ 的量级大小。
4.2 引理
给定N层DeepNet $F(x,\theta)(\theta=\{\theta_1,\theta_2,…,\theta_{2N}\})$,其中 $\theta_{2l-1}$ 和 $\theta_{2l}$ 分别表示第 $l$ 层下self-attention子层和FFN子层的参数。(注意:后续涉及层号的下标都是子层的编号,不再特殊说明)
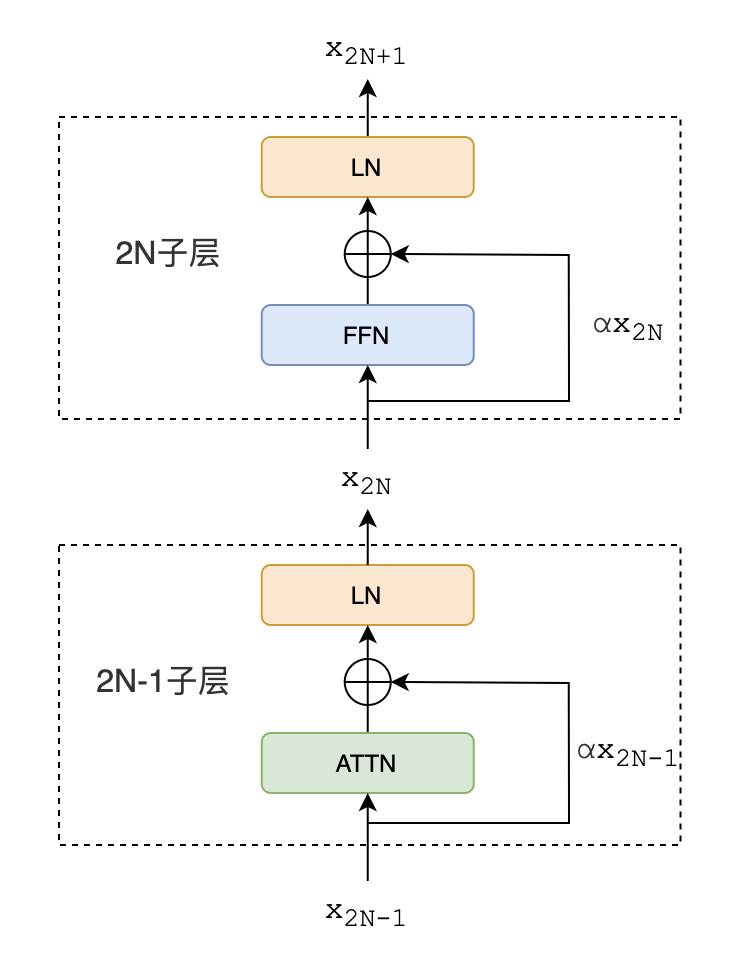
每个子层都通过DEEPNORM: $x_{l+1}=LN(\alpha x_l+G_l(x_l,\theta_l))$ 来归一化,则有
$$\Vert \Delta F\Vert \le\displaystyle\sum_{i=1}^{2N}\frac{\sqrt{v_i^2+w_i^2}}{\alpha}\Vert \theta_i^{\ast}-\theta_i\Vert $$
证明:
首先又是一番简化和假设,
每层输入 $x$ 的维度从 $d$ 维降到1维
$var(x+G_l(x))\overset{\mathrm\Theta}{=}var(x)+var(G_l(x))$
$v$ 和 $w$ 小于1,$\alpha$ 大于1
经过简化后,无论是self-attention子层还是FFN子层,$G(x)$ 都可以近似为 $G(x)\overset{\mathrm\Theta}{=}vwx$,即
$$x_{l+1}=f_l(x_l,\theta_l)=\displaystyle\frac{\alpha x_l+G_l(x_l)}{\sqrt{var(\alpha x_l+G_l(x_l))}}\overset{\mathrm\Theta}{=}\frac{\alpha+v_lw_l}{\sqrt{\alpha^2+v_l^2w_l^2}}x_l$$
求一下偏导数的近似:
$$\displaystyle\frac{\partial f_l}{\partial x_l}\overset{\mathrm\Theta}{=}\frac{\alpha+v_lw_l}{\sqrt{\alpha^2+v_l^2w_l^2}}\overset{\mathrm\Theta}{=}1$$
$$
\displaystyle\frac{\partial f_l}{\partial\theta_l}\overset{\mathrm\Theta}{=}(\frac{\partial f_l}{\partial v_l},\frac{\partial f_l}{\partial w_l})\overset{\mathrm\Theta}{=}\frac{\alpha x_l(\alpha-v_lw_l)}{(\alpha^2+v_l^2w_l^2)^{\frac{3}{2}}}(w_l,v_l)\overset{\mathrm\Theta}{=}\frac{x_l}{\alpha}(w_l,v_l)
$$
上面两公式最后的近似是我加上的,方便后面的推导。
【补充】
再补充一个论文中没有的:
$$E[\Vert \displaystyle\frac{\partial f_l}{\partial\theta_l}\Vert ^2]\approx E[x_l^2(v_l^2+w_l^2)/\alpha^2]=(v_l^2+w_l^2)/\alpha^2 E[x_l^2]=(v_l^2+w_l^2)/\alpha^2$$
因此可以认为
$$\Vert \displaystyle\frac{\partial f_l}{\partial\theta_l}\Vert \approx \sqrt{v_l^2+w_l^2}/\alpha$$
这就能解释为何论文中下面的推导 $\Vert \displaystyle\frac{\partial f}{\partial\theta}(x_{2N},\theta_{2N})\Vert $ 中的 $x_{2N}$ 项突然消失不见了。
开始计算,利用泰勒展开的一阶近似:
$$\Vert \Delta F\Vert =\Vert F(x,\theta^{\ast})-F(x,\theta)\Vert =\Vert x_{2N+1}^{\ast}-x_{2N+1}\Vert =\Vert f_{2N}(x_{2N}^{\ast},\theta_{2N}^{\ast})-f(x_{2N},\theta_{2N})\Vert $$
$$\approx \Vert \displaystyle\frac{\partial f}{\partial x}(x_{2N},\theta_{2N})(x_{2N}^{\ast}-x_{2N})+\frac{\partial f}{\partial\theta}(x_{2N},\theta_{2N})(\theta_{2N}^{\ast}-\theta_{2N})^T\Vert $$
$$\le\Vert \displaystyle\frac{\partial f}{\partial x}(x_{2N},\theta_{2N})\Vert \cdot\Vert x_{2N}^{\ast}-x_{2N}\Vert +\Vert \frac{\partial f}{\partial\theta}(x_{2N},\theta_{2N})\Vert \cdot\Vert \theta_{2N}^{\ast}-\theta_{2N}\Vert $$
$$\approx \Vert x_{2N}^{\ast}-x_{2N}\Vert +\displaystyle\frac{\sqrt{v_{2N}^2+w_{2N}^2}}{\alpha}\Vert \theta_{2N}^{\ast}-\theta_{2N}\Vert $$
继续递归下去,就可以得到:
$$\Vert \Delta F\Vert \le\displaystyle\sum_{i=1}^{2N}\frac{\sqrt{v_i^2+w_i^2}}{\alpha}\Vert \theta_i^{\ast}-\theta_i\Vert $$
证毕。
4.3 推导DEEPNORM参数
接下来我们让这个 $\Vert \Delta F\Vert $ 在SGD的每一步迭代中,和学习率 $\eta$ 在同一个数量级,而与网络层数N无关,即当 $\theta^{\ast}=\theta-\eta \displaystyle\frac{\partial L}{\partial\theta}$
时,有 $\Vert \Delta F\Vert =\mathcal O(\eta)$,这样就可以使得训练初始阶段,输出 $F$ 的变化幅度受控,跟网络层数N无关,达到我们初衷。
这里 $\displaystyle\frac{\partial L}{\partial\theta}$ 表示lost function对模型参数 $\theta$ 的导数。因此有
$$\displaystyle\Vert \theta_i^{\ast}-\theta_i\Vert =\eta\Vert \frac{\partial L}{\partial\theta_i}\Vert \le\eta\Vert \frac{\partial L}{\partial F}\Vert \cdot\Vert \frac{\partial F}{\partial\theta_i}\Vert $$
常见的任务都是输出 $F$ 之后接一个softmax之类的,假设 $\Vert \displaystyle\frac{\partial L}{\partial F}\Vert $ 有界是合理的,且一般与模型参数和层数N都无关,所以有 $\Vert \displaystyle\frac{\partial L}{\partial F}\Vert =\mathcal O(1)$
按照paper里的说法,根据参考文献[2]的结论有 $\Vert \displaystyle\frac{\partial F}{\partial\theta_i}\Vert \le\Vert \frac{\partial F}{\partial\theta_{2N}}\Vert \overset{\mathrm\Theta}{=}\sqrt{v_{2N}^2+w_{2N}^2}/\alpha$
【补充】
这篇参考文献[2]我去仔细看了,最后的数学推导有些语焉不详,不能让我信服,我们不妨自己推导一下:
$$\displaystyle\frac{\partial F}{\partial\theta_i}=\frac{\partial x_{2N+1}}{\partial\theta_i}=\frac{\partial x_{2N+1}}{\partial x_{2N}}\frac{\partial x_{2N}}{\partial x_{2N-1}}\cdots \frac{\partial x_{i+2}}{\partial x_{i+1}}\frac{\partial x_{i+1}}{\partial \theta_{i}}=(\prod_{l=i+1}^{2N}\frac{\partial x_{l+1}}{\partial x_{l}})\frac{\partial x_{i+1}}{\partial \theta_{i}}$$
这里涉及 $2N-i$ 项的导数连乘,我们需要更精确的量级估计。前面说过,paper中self-attention子层和FFN子层的函数 $G(x)$ 用 $vwx$ 来近似。这样做在量级估计上是合理的,但有个问题,输出 $G(x)$ 和输入 $x$ 的正负号永远一致,这是不合理的,根据在初始化阶段的对称性,应该一半概率同号,一半概率异号。我这里把它升级一下,改成 $G(x)\overset{\mathrm\Theta}{=}Ivwx$,即引入一个随机变量 $I$,0.5的概率为+1,0.5的概率为-1,因此有
$$x_{l+1}=f_l(x_l,\theta_l)=\displaystyle\frac{\alpha x_l+G_l(x_l)}{\sqrt{var(\alpha x_l+G_l(x_l))}}\overset{\mathrm\Theta}{=}\frac{\alpha+Iv_lw_l}{\sqrt{\alpha^2+v_l^2w_l^2}}x_l$$
$x_{l+1}$ 对 $x_l$ 的偏导数如下,按照论文后面的做法,令各层的 $v_l=v,w_l=w$,有
$$\displaystyle\frac{\partial x_{l+1}}{\partial x_{l}}\overset{\mathrm\Theta}{=}\frac{\alpha+Iv_lw_l}{\sqrt{\alpha^2+v_l^2w_l^2}}=\frac{\alpha+Ivw}{\sqrt{\alpha^2+v^2w^2}}$$
即可以认为在平均情况下,$2N-i$ 项的导数连乘项中,有一半的分子为 $\alpha+vw$,另一半的分子为 $\alpha-vw$,为简化推导,只考虑 $2N-i$ 为偶数的情况,令 $K=2N-i$,因此有
$$\displaystyle\prod_{l=i+1}^{2N}\frac{\partial x_{l+1}}{\partial x_{l}}\overset{\mathrm\Theta}{=}\frac{(\alpha+vw)^{K/2}(\alpha-vw)^{K/2}}{(\alpha^2+v^2w^2)^{K/2}}=\frac{(\alpha^2-v^2w^2)^{K/2}}{(\alpha^2+v^2w^2)^{K/2}}=(\frac{\alpha^2-v^2w^2}{\alpha^2+v^2w^2})^{K/2}\lt 1$$
可以看到,随着层号 $i$ 变小,即 $K$ 变大,上式指数衰减,跟参考文献[2]中的结论一致。
对于 $\displaystyle\frac{\partial x_{l+1}}{\partial\theta_l}$,也会变成
$$\displaystyle\frac{\partial x_{l+1}}{\partial\theta_l}=\frac{\partial f_l}{\partial\theta_l}\overset{\mathrm\Theta}{=}(\frac{\partial f_l}{\partial v_l},\frac{\partial f_l}{\partial w_l}) \overset{\mathrm\Theta}{=}\frac{\alpha x_l(I\alpha-v_lw_l)}{(\alpha^2+v_l^2w_l^2)^{\frac{3}{2}}}(w_l,v_l)\overset{\mathrm\Theta}{=}\frac{Ix_l}{\alpha}(w_l,v_l)$$
$$\displaystyle E[\Vert \frac{\partial x_{l+1}}{\partial\theta_l}\Vert ^2]\overset{\mathrm\Theta}{=}E[I^2x_l^2(v_l^2+w_l^2)/\alpha^2]=(v_l^2+w_l^2)/\alpha^2 E[x_l^2]=(v_l^2+w_l^2)/\alpha^2=(v^2+w^2)/\alpha^2$$
因此可以认为 $\displaystyle\Vert \frac{\partial x_{l+1}}{\partial\theta_l}\Vert \overset{\mathrm\Theta}{=}\sqrt{v^2+w^2}/\alpha$,跟前面结论一致。
综上,就有
$$\displaystyle\Vert \frac{\partial F}{\partial\theta_i}\Vert \le\Vert \prod_{l=i+1}^{2N}\frac{\partial x_{l+1}}{\partial x_l}\Vert \cdot\Vert \frac{\partial x_{i+1}}{\partial\theta_i}\Vert \le\Vert \frac{\partial x_{i+1}}{\partial\theta_i}\Vert \overset{\mathrm\Theta}{=}\sqrt{v^2+w^2}/\alpha\overset{\mathrm\Theta}{=}\Vert \frac{\partial F}{\partial\theta_{2N}}\Vert $$
这样就跟paper中结论一致了。
继续顺着paper的思路,有了引理4.2,再根据上面的分析,就有
$$\displaystyle\Vert \Delta F\Vert \le\sum_{i=1}^{2N}\frac{\sqrt{v_i^2+w_i^2}}{\alpha}\Vert \theta_i^{\ast}-\theta_i\Vert \le\eta\sum_{i=1}^{2N}\frac{\sqrt{v_i^2+w_i^2}}{\alpha}\Vert \frac{\partial L}{\partial F}\Vert \cdot\Vert \frac{\partial F}{\partial\theta_i}\Vert \le\mathcal O(\eta\sum_{i=1}^{2N}(\frac{\sqrt{v_i^2+w_i^2}}{\alpha})^2=\mathcal O(\eta\cdot2N\frac{v^2+w^2}{\alpha^2})$$
因此只需要让 $\displaystyle 2N\frac{v^2+w^2}{\alpha^2}=1$,即可满足 $\Vert \Delta F\Vert =\mathcal O(\eta)$,论文中令 $\alpha=(2N)^{1/4},v=w=\beta=(8N)^{-1/4}$ ,这就是本文开头表格中两个参数 $\alpha,\beta$ 取值的来历。
【补充】
看起来 $\alpha,\beta$ 的取法还可以有其他形式,论文中也没有详细说当前这种取值的原因,只说是为了平衡残差连接和初始化的影响。我们可以试着猜测一下。
回过头来看一下 $\theta_i$ 的SGD更新过程:$\displaystyle\Vert \Delta\theta_i\Vert =\Vert \theta_i^{\ast}-\theta_i\Vert =\eta\Vert \frac{\partial L}{\partial\theta_i}\Vert =\mathcal O(\eta\frac{\Vert \theta_i\Vert }{\alpha})$,如果 $\alpha$ 太小,则 $\theta_i$ 更新过快,没迭代几步就大幅偏离我们精心设计的初始值,影响千层大业;如果 $\alpha$ 太大,则可能收敛太慢,得不偿失。
考虑到初始阶段 $\Vert \theta_i\Vert \ll1$ ,是一个很小的值,我们不妨将 $1/\alpha$ 设为初始化阶段的 $\Vert \theta_i\Vert $,得到 $\Vert \Delta\theta_i\Vert =\mathcal O(\eta\displaystyle\Vert \theta_i\Vert ^2)$,而 $\Vert \theta_i\Vert ^2$ 是比 $\Vert \theta_i\Vert $ 更小的值,这样更新量看起来比较适中,因此有 $1/\alpha=\Vert \theta_i\Vert =\sqrt{v^2+w^2}=\sqrt2\beta$,代入 $\displaystyle 2N\frac{v^2+w^2}{\alpha^2}=2N\frac{\beta^2+\beta^2}{\alpha^2}=1$,正好得到 $\alpha=(2N)^{1/4},v=w=\beta=(8N)^{-1/4}$,完美。
5. One More Thing,直接矩阵版的推导【补充】
看完论文,一边赞叹,一边却又总感觉不踏实。论文中把向量和矩阵都简化成标量来推导真的合理吗?难道在实际情况下,$\alpha$ 和 $\beta$ 的取值与输入向量的维度以及参数矩阵的维度一点关系没有?还有multi-head降为1-head不影响结论?想不明白那就直接推一把。
想一下真实场景包含2N个子层的Transformer网络,第 $l$ 层的输入为 $n\times d$ 矩阵 $X_l$,包含n个d维向量 $\mathbf x_{l,p}$,$p=1,2,…,n$,输出同样为 $n\times d$ 矩阵 $X_{l+1}$,包含n个d维向量 $\mathbf x_{l+1,p}$,$p=1,2,…,n$,所以网络最后的输出 $F=X_{2N+1}$,同样是一个 $n\times d$ 矩阵。
我们用 $\Delta F$ 的Frobenius范数 $\Vert \Delta F\Vert _F$ 来估计大小,而 $\Vert \Delta F\Vert _F^2=\displaystyle\sum_{p=1}^n\Vert \Delta\mathbf x_{2N+1,p}\Vert _2^2\le(\sum_{p=1}^n\Vert \Delta \mathbf x_{2N+1,p}\Vert _2)^2$,因此有 $\displaystyle\Vert \Delta F\Vert _F\le\sum_{p=1}^n\Vert \Delta\mathbf x_{2N+1,p}\Vert _2$
我们可以先估计右边任意一项 $\Vert \Delta\mathbf x_{2N+1,p}\Vert _2$ 的大小。因为是任意项,下面推导省略下标 $p$。
因为有两种子层,FFN和Attention,我们分两种情况讨论:
5.1 FFN子层
一些设定:
层号为偶数的都是FFN子层,如最后一层,层号为2N,输入为 $\mathbf x_{2N}$,输出为 $\mathbf x_{2N+1}$,就是一个FFN子层。考虑任意一个FFN子层,输入行向量用 $\mathbf x$ 表示,输出行向量用 $\mathbf x_{l+1}=f(\mathbf x,\theta)$ 表示。
由于输入 $\mathbf x$ 来自于下面一层的输出,经过了LN函数,所以 $\mathbf x$ 的每个元素 $x_i$,有 $E[x_i]=0,E[x_i^2]=1$。我们假定第一层的输入也符合,这也是比较合理的,第一层输入来自于word embedding初始化和position embedding初始化的叠加,仍然可以是正态分布,那么就可以选择合适的参数使其符合。
将子层的前向计算分解如下:
$$\mathbf x_{l+1}=f(\mathbf x,\theta)=\mathrm{LN}(\mathbf z)$$
$$\mathbf z=\alpha\mathbf x+\mathrm{FFN}(\mathbf x,\theta)=\alpha\mathbf x+\mathrm{ReLU}(\mathbf xW)V$$
其中 $W\in\mathbf R^{d\times m}$,$V\in\mathbf R^{m\times d}$,一般有 $m\ge d$,我们定义一个算子 $vec$ ,$vec(W)$ 表示把矩阵 $W$ 展开为行向量,则网络参数可以统一写成行向量形式: $\theta=(vec(V),vec(W))$。根据我们前面介绍的xavier normal初始化,$W$ 的每一个元素 $w_{ij}\sim N(0,2w^2/d)$,即有 $E(w_{ij})=0,E(w_{ij}^2)=2w^2/d$,同样 $V$ 的每一个元素 $v_{ij}\sim N(0,v^2/m)$,$E(v_{ij})=0,E(v_{ij}^2)=v^2/m$。$\alpha$,$v$ 和 $w$ 即为我们最终要确定的参数。
$\mathbf z$ 的任意元素 $z_i$ 为:
$$\displaystyle z_i=\alpha x_i+\sum_{j=1}^d\sum_{k=1}^m x_jw_{jk}v_{ki}R_k$$
其中 $R_k$ 为随机变量,取值为1或0,表示ReLU函数的第 $k$ 维标量输入是否大于0,根据初始化阶段的对称性,$R_k$ 取1和0的概率均为0.5。
计算偏导数:
我们把 $\mathbf z$ 函数的Jacobian矩阵的每一个元素都单独写出来:
$$\displaystyle\frac{\partial z_i}{\partial x_j}=\delta_{ij}\alpha+\sum_{k=1}^m w_{jk}v_{ki}R_k$$
当 $i=j$ 时,$\delta_{ij}=1$,否则 $\delta_{ij}=0$。
$$\displaystyle\frac{\partial z_i}{\partial v_{ki}}=\sum_{j=1}^d x_jw_{jk}R_k$$
$$\displaystyle\frac{\partial z_i}{\partial v_{kj}}=0,if\,j\ne i$$
$$\displaystyle\frac{\partial z_i}{\partial w_{jk}}=x_jv_{ki}R_k$$
而对于LN函数,根据参考文献[2]的结论,有
$$\displaystyle\Vert \frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\Vert _2\approx\frac{\sqrt{d}}{\Vert \mathbf z\Vert _2}$$
注意,上式左边Jacobian矩阵的norm为谱范数(Spectral Norm),不是Frobenius范数。
对于 $\mathbf z$ 的元素 $z_i$,再写一遍表达式:
$$\displaystyle z_i=\alpha x_i+\sum_{j=1}^d\sum_{k=1}^m x_jw_{jk}v_{ki}R_k$$
我们可以计算得到
$$E[z_i]=0$$
$$\displaystyle E[z_i^2]=\alpha^2 E[x_i^2]+\frac{1}{2}\sum_{j=1}^d\sum_{k=1}^m E[x_j^2]E[w_{jk}^2]E[v_{ki}^2]$$
$$\displaystyle=\alpha^2+\frac{1}{2}dm\frac{2w^2}{d}\frac{v^2}{m}=\alpha^2+v^2w^2$$
$$E[\Vert \mathbf z\Vert _2^2]=dE[z_i^2]=d(\alpha^2+v^2w^2)$$
因此我们认为 $\Vert \mathbf z\Vert _2\approx\sqrt{d(\alpha^2+v^2w^2)}$
所以有$\displaystyle\Vert \frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\Vert _2\approx\frac{\sqrt{d}}{\Vert \mathbf z\Vert _2}\approx\frac{1}{\sqrt{\alpha^2+v^2w^2}}$
后面我们会多次用到这种通过期望来估计大小的方法。
计算输出增幅:
$$\Vert \Delta \mathbf x_{l+1}\Vert _2=\Vert \mathbf x_{l+1}^{\ast}-\mathbf x_{l+1}\Vert _2=\Vert f(\mathbf x^{\ast},\theta^{\ast})-f(\mathbf x,\theta)\Vert _2$$
$$\displaystyle\approx\Vert \frac{\partial f}{\partial \mathbf x}(\mathbf x,\theta)\Delta\mathbf x^T+\frac{\partial f}{\partial vec(V)}(\mathbf x,\theta)\Delta vec(V)^T+\frac{\partial f}{\partial vec(W)}(\mathbf x,\theta)\Delta vec(W)^T\Vert _2$$
$$\displaystyle=\Vert \frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T+\frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T\Vert _2$$
$$\displaystyle\le\Vert \frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\Vert _2\cdot\Vert \frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T\Vert _2+\Vert \frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\Vert _2\cdot\Vert \frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T\Vert _2$$
(1) 先看 $\displaystyle\Vert \frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T\Vert _2$ 这一项:
$$\displaystyle(\frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T)_i=\sum_{j=1}^d\frac{\partial z_i}{\partial x_j}\Delta x_j=\alpha\Delta x_i+\sum_{j=1}^d\sum_{k=1}^m w_{jk}v_{ki}R_k\Delta x_j$$
$$\displaystyle E[(\frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T)_i^2]=\alpha^2E[(\Delta x_i)^2]+\sum_{j=1}^d\sum_{k=1}^m\frac{1}{2}E[w_{jk}^2]E[v_{ki}^2]E[(\Delta x_j)^2]$$
$$\displaystyle=\alpha^2E[(\Delta x_i)^2]+\sum_{j=1}^dE[(\Delta x_j)^2]\frac{1}{2}m\frac{v^2}{m}\frac{2w^2}{d}$$
$$\displaystyle=\alpha^2E[(\Delta x_i)^2]+\frac{v^2w^2}{d}\sum_{j=1}^dE[(\Delta x_j)^2]$$
$$\displaystyle E[\Vert \frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T\Vert _2^2]=\sum_{i=1}^dE[(\frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T)_i^2]=\alpha^2\sum_{i=1}^dE[(\Delta x_i)^2]+v^2w^2\sum_{j=1}^dE[(\Delta x_j)^2]$$
$$\displaystyle=(\alpha^2+v^2w^2)\sum_{i=1}^dE[(\Delta x_i)^2]=(\alpha^2+v^2w^2)E[\Vert \Delta\mathbf x\Vert _2^2]$$
所以 $\displaystyle\Vert \frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T\Vert _2\approx\sqrt{\alpha^2+v^2w^2}\Vert \Delta\mathbf x\Vert _2$
(2) 再看 $\displaystyle\Vert \frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T\Vert _2$ 这一项:
$$\displaystyle(\frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T)_i=\sum_{k=1}^m\frac{\partial z_i}{\partial v_{ki}}\Delta v_{ki}+\sum_{j=1}^m\sum_{k=1}^d\frac{\partial z_i}{\partial w_{jk}}\Delta w_{jk}$$
$$\displaystyle=\sum_{k=1}^m\sum_{j=1}^d x_jw_{jk}R_k\Delta v_{ki}+\sum_{j=1}^m\sum_{k=1}^dx_jv_{ki}R_k\Delta w_{jk}$$
可算出:
$$\displaystyle E[(\frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T)_i^2]=w^2\sum_{k=1}^mE[(\Delta v_{ki})^2]+\frac{1}{2m}v^2E[\Vert \Delta vec(W)\Vert_2^2]$$
因此有
$$\displaystyle E[\Vert \frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T\Vert _2^2]=\sum_{i=1}^dw^2\sum_{k=1}^mE[(\Delta v_{ki})^2]+\sum_{i=1}^d\frac{1}{2m}v^2E[\Vert \Delta vec(W)\Vert_2^2]$$
$$\displaystyle=w^2E[\Vert \Delta vec(V)\Vert _2^2]+\frac{dv^2}{2m}E[\Vert \Delta vec(W)\Vert_2^2]$$
$$\displaystyle\le w^2E[\Vert \Delta vec(V)\Vert _2^2]+v^2E[\Vert \Delta vec(W)\Vert_2^2]$$
$$\lt (v^2+w^2)E[\Vert \Delta vec(V)\Vert _2^2+\Vert \Delta vec(W)\Vert_2^2]$$
$$=(v^2+w^2)E[\Vert \Delta \theta\Vert _2^2]$$
【注意这里是刻意凑出和论文一样的结果,其实如果事先设定 $v=w=\beta$,这里上界可以更小,为: $\beta ^2E[\Vert \Delta \theta\Vert _2^2]$ 】
所以 $\displaystyle\Vert \frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T\Vert _2\approx\sqrt{v^2+w^2}\Vert \Delta\theta\Vert _2$
(3) 最后整合组装一下:
$$\Vert \Delta \mathbf x_{l+1}\Vert _2=\Vert \mathbf x_{l+1}^{\ast}-\mathbf x_{l+1}\Vert _2$$
$$\displaystyle\le\Vert \frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\Vert _2\cdot\Vert \frac{\partial \mathbf z}{\partial \mathbf x}\Delta\mathbf x^T\Vert _2+\Vert \frac{\partial\mathrm{LN}(\mathbf z)}{\partial\mathbf z}\Vert _2\cdot\Vert \frac{\partial \mathbf z}{\partial vec(V)}\Delta vec(V)^T+\frac{\partial \mathbf z}{\partial vec(W)}\Delta vec(W)^T\Vert _2$$
$$\displaystyle\approx\frac{1}{\sqrt{\alpha^2+v^2w^2}}(\sqrt{\alpha^2+v^2w^2}\Vert \Delta\mathbf x\Vert _2+\sqrt{v^2+w^2}\Vert \Delta\theta\Vert _2)$$
$$\displaystyle=\Vert \Delta\mathbf x\Vert _2+\frac{\sqrt{v^2+w^2}}{\sqrt{\alpha^2+v^2w^2}}\Vert \Delta\theta\Vert _2$$
$$\displaystyle\lt \Vert \Delta\mathbf x\Vert _2+\frac{\sqrt{v^2+w^2}}{\alpha}\Vert \Delta\theta\Vert _2$$
(4) 补上完整的层号下标,就是:
$$\Vert \Delta \mathbf x_{l+1}\Vert _2=\Vert \mathbf x_{l+1}^{\ast}-\mathbf x_{l+1}\Vert _2$$
$$\displaystyle\le\Vert \Delta\mathbf x_l\Vert _2+\frac{\sqrt{v^2+w^2}}{\alpha}\Vert \Delta\theta_l\Vert _2$$
$$\displaystyle=\Vert \mathbf x_{l}^{\ast}-\mathbf x_{l}\Vert _2+\frac{\sqrt{v^2+w^2}}{\alpha}\Vert \theta_{l}^{\ast}-\theta_{l}\Vert _2$$
5.2 Attention子层
呃,敲公式快把手敲断了,实在没有勇气再推导Attention的完整形式,偷个懒,仿照论文里的处理,Attention的函数用 $\mathrm{Attn}(Q,K,V)\overset{\mathrm\Theta}{=}VW^VW^O$ 代替。
层号为奇数的都是Attention子层,如倒数第二层,层号为2N-1,输入为 $\mathbf x_{2N-1}$,输出为 $\mathbf x_{2N}$,就是一个Attention子层。考虑任意一个Attention子层,输入行向量用 $\mathbf x_l$ 表示,输出行向量用 $\mathbf x_{l+1}$ 表示。函数为:
$$\mathbf x_{l+1}=\mathrm{LN}(\alpha\mathbf x_l+\mathrm{Attn}(\mathbf x_l))\approx\mathrm{LN}(\alpha\mathbf x_l+\mathbf x_lW^{V,l}W^{O,l})$$
考虑multi-head的情况,Attn无非变成了 $\mathbf x_l(W_1^{V,l},W_2^{V,l},…,W_h^{V,l})W^{O,l}$,我们将 $(W_1^{V,l},W_2^{V,l},…,W_h^{V,l})$ 整体看作 $W^{V,l}$,依然是上面的形式。
这就跟FFN的式子很像了,网络参数 $\theta_l=(vec(W^{V,l}),vec(W^{O,l}))$ ,推导过程中少了随机变量 $R_k$,更简单。完全类似的过程,同样有
$$\Vert \Delta \mathbf x_{l+1}\Vert _2=\Vert \mathbf x_{l+1}^{\ast}-\mathbf x_{l+1}\Vert _2$$
$$\displaystyle\le\Vert \Delta\mathbf x_l\Vert _2+\frac{\sqrt{v^2+w^2}}{\alpha}\Vert \Delta\theta_l\Vert _2$$
$$\displaystyle=\Vert \mathbf x_{l}^{\ast}-\mathbf x_{l}\Vert _2+\frac{\sqrt{v^2+w^2}}{\alpha}\Vert \theta_{l}^{\ast}-\theta_{l}\Vert _2$$
5.3 完结
结合5.1和5.2,我们就有
$$\Vert \Delta\mathbf x_{2N+1}\Vert_2\le\displaystyle\sum_{i=1}^{2N}\frac{\sqrt{v^2+w^2}}{\alpha}\Vert \theta_i^{\ast}-\theta_i\Vert_2$$
跟论文引理4.2就一致了。后面的过程一模一样,不再赘述。
最后对比一下,严格来说,完整的输出 $\displaystyle\Vert \Delta F\Vert _F\le\sum_{p=1}^n\Vert \Delta\mathbf x_{2N+1,p}\Vert _2$,跟输入序列长度n相关,这点论文中没有体现。还有,前面5.1的上限推导,如果用 $\beta^2$ 代替 $v^2+w^2$,那么最后推出来的 $\alpha$ 和 $\beta$ 取值会不太一样。
参考文献
[1] DeepNet: Scaling Transformers to 1,000 Layers https://arxiv.org/abs/2203.00555
[2] On Layer Normalization in the Transformer Architecture https://arxiv.org/abs/2002.04745