MLR, PLM

前言

　　最近阿里的盖坤大神放出了一篇论文Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction，介绍了阿里广告的一个主要ctr预估模型Large Scale Piece-wise Linear Model (LS-PLM)，在2012年就开始使用，据说早期叫做Mixture of LR(MLR)。

　　看完论文就很想验证一下效果，于是基于原来的alphaFM代码很快就实现了一个单机多线程版本，优化算法用了FTRL。完成代码的时候正好又赶上alphaGo完虐人类，于是命名仍然冠以alpha，叫做alphaPLM。

　　代码地址在：
　　https://github.com/CastellanZhang/alphaPLM

算法原理

　　PLM可以看做是混合了聚类和分类的思想，即将特征空间分片或者说分区间，每个分片就是一个聚类，每个聚类对应一个单独的线性模型LR。这里的聚类是软聚类，即每个样本可以属于多个分片，有概率分布。最后计算ctr是先算出在每个分片的ctr，再按属于各个分片的概率加权平均。通过分片线性拟合，达到了非线性的效果。

　　具体模型公式如下：

$$
p(y=1|x)=\sum_{i=1}^{m}\frac{e^{u_i^Tx}}{\sum_{j=1}^me^{u_j^Tx}}\cdot\frac{1}{1+e^{-w_i^Tx}}\\
=\sum_{i=1}^{m}\frac{e^{u_i^Tx}}{\sum_{j=1}^me^{u_j^Tx}}\cdot\sigma(w_i^Tx)
$$

　　可以看到，聚类部分是用了softmax函数，分类部分就是LR的sigmoid函数。该算法的巧妙之处就是将二者合成一个公式，一起训练参数。公式中m是分片数，属于超参数，由人工给定。模型参数是 $\Theta=\{u_1,…,u_m,w_1,…,w_m\}\in R^{d\times 2m}$，需要训练得到。

　　论文中的优化方法采用的是LBFGS，实现起来比较复杂，我为了快速验证算法效果，优化改成了FTRL，需要计算损失函数对u和w的梯度，下面给出推导。

　　首先对于 $y\in\{-1,1\}$，模型可以统一形式：

$$
p(y|x)=\sum_{i=1}^{m}\frac{e^{u_i^Tx}}{\sum_{j=1}^me^{u_j^Tx}}\cdot\frac{1}{1+e^{-yw_i^Tx}}\\
=\sum_{i=1}^{m}\frac{e^{u_i^Tx}}{\sum_{j=1}^me^{u_j^Tx}}\cdot\sigma(yw_i^Tx)
$$

　　单条样本(x,y)的损失函数：
$$
l(\Theta|x,y)=-\ln P(y|x,\Theta)=-\ln\frac{1}{\sum_{j=1}^me^{u_j^Tx}}\sum_{i=1}^{m}e^{u_i^Tx}\sigma(yw_i^Tx)\\
=\ln\sum_{j=1}^me^{u_j^Tx}-\ln(\sum_{i=1}^{m}e^{u_i^Tx}\sigma(yw_i^Tx))
$$
　　梯度计算：
$$
\nabla_{u_k}l=\frac{e^{u_k^Tx}x}{\sum_{j=1}^me^{u_j^Tx}}-\frac{e^{u_k^Tx}\sigma(yw_k^Tx)x}{\sum_{i=1}^{m}e^{u_i^Tx}\sigma(yw_i^Tx)}
$$
$$
\nabla_{w_k}l=\frac{ye^{u_k^Tx}\sigma(yw_k^Tx)(\sigma(yw_k^Tx)-1)x}{\sum_{i=1}^{m}e^{u_i^Tx}\sigma(yw_i^Tx)}
$$
　　后续的FTRL算法框架和alphaFM非常类似，不再详述，可以参见之前的文档和实现代码。

算法效果

　　论文中给了一个demo数据的例子，如下图：

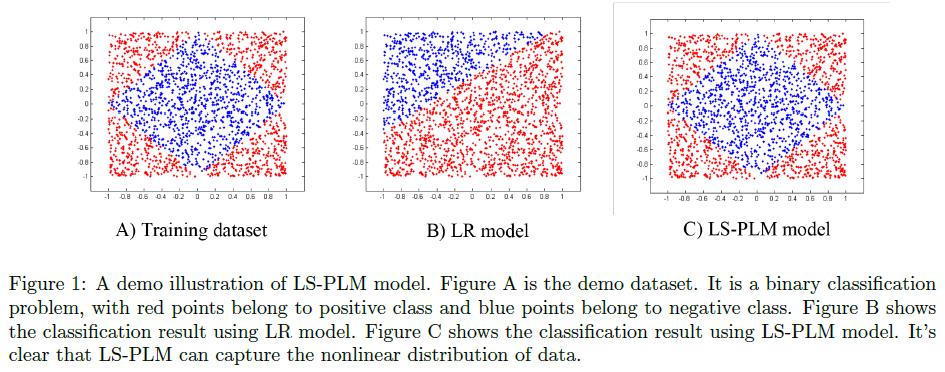
　　我们可以通过代码生成类似的样本，来验证一下算法效果：

#demo_data1.py
import sys
from random import random

n = int(sys.argv[1])

for i in range(n):
    x = 2 * random() - 1.0
    y = 2 * random() - 1.0
    label = 1
    if abs(x) + abs(y) < 1.0:
        label = 0
    print str(label) + " x:" + str(x) + " y:" + str(y)

　　生成1万条训练样本和2000条测试样本：

　　python demo_data1.py 10000 > train.txt

　　python demo_data1.py 2000 > test.txt

　　alphaPLM的训练参数如下：

　　cat train.txt | ./plm_train -m model.txt -u_bias 1 -w_bias 1 -u_l1 0.001 -u_l2 0.1 -w_l1 0.001 -w_l2 0.1 -core 1 -piece_num 4 -u_stdev 1 -w_stdev 1 -u_alpha 10 -w_alpha 10

　　在测试集的AUC可以达到0.99以上。

　　如果是LR或FM，你会发现无论你怎么调参，AUC始终在0.5左右。

　　直观上也很容易理解，看图就会发现，如果特征就是x和y的坐标值的话，数据非线性可分，而很明显在四个象限的分片里分别都是线性可分的。

　　你心里是否已经忍不住开始唾弃LR：“啊呸，LR果然是个战五渣！连这么个demo数据都搞不定！”那你可就冤枉LR了，原始特征非线性，完全可以通过转换变成线性或近似线性，比如做个简单的离散化就会大不一样：

#demo_data2.py
import sys
from random import random

n = int(sys.argv[1])

for i in range(n):
    x = 2 * random() - 1.0
    y = 2 * random() - 1.0
    label = 1
    if abs(x) + abs(y) < 1.0:
        label = 0
    fx = "x" + str(int(x*10)) + ":1"
    fy = "y" + str(int(y*10)) + ":1"
    print str(label) + " " + fx + " " + fy

　　重新生成1万条训练样本和2000条测试样本：

　　python demo_data2.py 10000 > train.txt

　　python demo_data2.py 2000 > test.txt

　　此时你会发现，无论LR、FM还是PLM，AUC都很容易达到0.99以上。

　　而在我们广告业务的真实数据中，LR所面对的几乎都是千万维或上亿维的高维离散特征，效果并不会比FM或PLM差太多。我在真实数据的实验也验证了这一点，PLM和FM相比LR提升的都差不多，AUC基本都是在千分位提高几个点。

lambdaFM

Ensembling, Lagrange