论文学习:OCPC, ROI
前言
翻 KDD2017的论文,又瞅见了阿里的这篇Optimized Cost per Click in Taobao Display Advertising,好文章常看常新,重看一遍写个学习笔记,同时把论文里省略的证明补充一下。
这篇论文详细介绍了阿里展示广告的OCPC(Optimized Cost per Click)机制,以手机淘宝首页的Banner广告(Banner CPC Ads,广告可以是商品、店铺或品牌)和猜你喜欢版块的广告(Item CPC Ads,猜你喜欢200个推荐位里包含3个广告位都是具体商品)为例。
广告系统是一个三方博弈的生态,要同时兼顾用户体验、广告主利益、平台收入三方的诉求。淘宝广告的计费方式为CPC,即广告主事先设定单次点击出价bid price,每次请求来了广告系统预测用户点击概率pCTR,然后按照bid*pCTR即eCPM排序,分数高的广告获得展示,如果用户点击了广告则广告平台获得广告主的费用bid price(为了简化问题暂先忽略GSP的影响)。
按照这种方式主要是以广告平台的收入为优化目标,广告主即便出高价获得了流量但是ROI没法保证,即流量质量没法保证。广告主可以对不同的广告位不同的人群设定不同的出价来缓解,但粒度还是太粗了,如果广告系统能在每次请求这个细粒度上根据pCVR来帮助广告主自动调整出价就完美了,即pCVR高的请求出价高,pCVR低的请求出价低,保证ROI不会降,这就是OCPC的核心思想。
淘宝的广告主还有一个特点,他们本身就是淘宝的商家,且大部分是中小商家,GMV是他们的最重要诉求,广告预算一般都是占他们GMV的固定比例,因此提高GMV还能带来广告预算的增长,对广告平台的长期发展也是有利的。GMV提高一定程度上也反映了用户体验的提高,毕竟你推的广告被用户相中了还消费了。
至此,算法的框架已经基本成型:以ROI不降为约束,通过算法自动调整出价来尽量优化eCPM和GMV。
算法细节
1. 先给出一系列定义
- 定义用户$u$在点击广告$a$之后发生交易转化事件$c$的概率为$p(c|u,a)$,也就是所谓的从点击到购买的转化率CVR。
- 定义$v_a$为广告商品$a$的pay-per-buy(PPB),也就是商家的收入,因此单次点击的期望GMV为$p(c|u,a)*v_a$。
- 用户$u$对广告$a$的单次点击的期望ROI,这里忽略GSP的影响:
$$
roi_{(u,a)}=\frac{p(c|u,a)*v_a}{b_a}
$$ - 广告$a$在一段时间内总的期望ROI为:
$$
roi_a=\frac{v_a\cdot\sum_u n_u\cdot p(c|u,a)}{b_a\cdot\sum_u n_u}=\frac{E_u[p(c|u,a)]\cdot v_a}{b_a}
$$
其中$n_u$为一段时间内用户$u$对广告$a$的点击次数。$E_u[p(c|u,a)]$ 的计算可以通过一段时间内预测模型给出的广告$a$所有pCVR值求均值得到,但要去除最大10%和最小10%的pCVR值,目的应该是去除异常点,使结果更加准确可靠。
2. bid优化的上下界
$roi_a$与$E_u[p(c|u,a)]$ 成线性关系,对于单次请求,假设出价从$b_a$调整为$b_a^*$,只要满足
$$
\frac{b_a^*}{b_a}\le\frac{p(c|u,a)}{E_u[p(c|u,a)]}
$$
即能保证$roi_a$不降。
论文给出的最终上下界如下,其实在其中考虑商业利益做了一定的妥协,并不能保证所有广告的ROI都一定不降,论文后面的实验结果也说明了这一点,大部分广告的ROI都有提高,少部分有降,但总体还是提高了,
$$
l(b_a^*)=
\begin{cases}
b_a\cdot(1-r_a), & \frac{p(c|u,a)}{E_u[p(c|u,a)]}<1 \\
b_a, & \frac{p(c|u,a)}{E_u[p(c|u,a)]}\ge 1 \\
\end{cases} \\
u(b_a^*)=
\begin{cases}
b_a, & \frac{p(c|u,a)}{E_u[p(c|u,a)]}<1 \\
b_a\cdot\min(1+r_a,\frac{p(c|u,a)}{E_u[p(c|u,a)]}), & \frac{p(c|u,a)}{E_u[p(c|u,a)]}\ge 1 \\
\end{cases}
$$
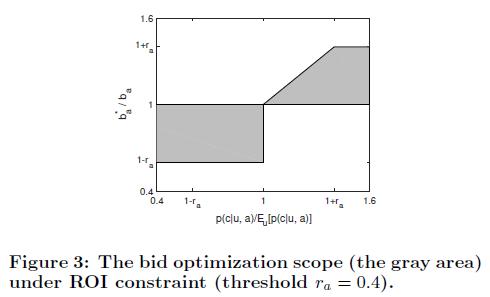
其中$l(b_a^*)$ 为下限,$u(b_a^*)$ 为上限,还有个上下浮动的阈值参数$r_a$(比如40%),看下图更加明显,灰色区域为$b_a^*$ 的候选取值范围,即所谓的可行域(feasible region)。可以看到当流量质量较差时,$b_a^*$ 的上限还能到$b_a$ 本身,这显然是不能保证ROI不降的,这里做了妥协。
3. Ranking
在依赖eCPM的排序机制下,在可行域内选取不同的$b_a^*$ 可能会导致排序结果的不同,进而影响到其他的指标。
先看最简单的情况,只有1个广告位,候选广告集合A中共有n个广告,通过调整出价来竞争这个广告位,优化问题的数学形式如下:
$$
\max_{b_1^*,\cdots,b_n^*}f(k,b_k^*)\qquad\qquad\qquad\qquad \\
s.t.\qquad k=\mathop{\arg\max}_i\ pctr_i*b_i^* \\
\qquad\qquad l(b_i^*)\le b_i^*\le u(b_i^*),\forall i\in A
$$
$k$是最终胜出的广告,依赖于$b_1^*,\cdots,b_n^*$ 的选取,$f(\cdot)$ 是需要优化的目标函数,综合了我们关注的指标。比如下面两个例子:
$$
f_1(k,b_k^*)=pctr_k*pcvr_k*v_k\qquad\qquad\qquad \\
f_2(k,b_k^*)=pctr_k*pcvr_k*v_k+\alpha*pctr_k*b_k^*
$$
$f_1$只考虑GMV,而$f_2$同时考虑GMV和eCPM即广告平台收入。论文后面的实验部分给出了一种更复杂的形式,同样是综合GMV和eCPM:
$$
f(k,b_k^*)=pctr_k*b_k^**(1+\sigma(\frac{pcvr_k*v_k*||A||}{\sum_{i\in A}pcvr_i*v_i},w)*r_a)
$$
其中$w=6$,$r_a=0.4$,$\sigma(x,w)=\frac{x^w-1}{x^w+1}$,当$w>0$时,$\sigma(x,w)$ 是一个关于$x$的值域范围(-1,1)的单调增函数。
以上所有的$f(k,b_k^*)$ 函数都是$b_k^*$ 的单调增函数(更准确的说应该是单调非减函数,论文里没有严格区分),这为后面的ranking算法提供了便利。一般来说,这个单调增的假设也是合理的,毕竟出价高了对于大部分指标都是好事。
- 优化问题求解方法:
设$s_a^*=pctr_a*b_a^*$,则$s_a^*$ 的下界和上界分别为$l(s_a^*)=pctr_a*l(b_a^*)$,$u(s_a^*)=pctr_a*u(b_a^*)$,将所有的$f(i,u(b_i^*))$ 按降序排列,然后按顺序找出第一个广告$k$,满足$u(s_k^*)$ 大于等于其他所有的$l(s_i^*)$,这个$k$就是最终展示的广告,且$b_k^*=u(b_k^*)$。 - 论文省略了求解方法正确性的严格证明,这里补充一下:
a. 首先最终结果$b_k^*$ 一定等于$u(b_k^*)$。
反证法:假设最终结果为$b_k^*$,且 $b_k^*\lt u(b_k^*)$ 。由约束可知 $pctr_k*b_k^*$ 大于等于其他所有的$pctr_i*b_i^*$,若取新的$b_k^{+}=u(b_k^*)$,则有$pctr_k*b_k^{+}>pctr_k*b_k^*$,$pctr_k*b_k^{+}$ 仍然大于等于其他所有的$pctr_i*b_i^*$,即最终胜出的广告还是$k$,但由$f(\cdot)$ 的单调递增性,$f(k,b_k^{+})>f(k,b_k^*)$,矛盾。
b. 由a可知,$f(\cdot)$ 的最大值一定是某个$f(i,u(b_i^*))$,$i$从1到$n$。我们当然希望越大越好,因此从大到小排列挨个检验,$f(k,u(b_k^*))$ 能雀屏中选的前提是$u(b_k^*)$ 实力够硬,能够在其他$b_i^*$ 配合的情况下满足约束条件:$pctr_k*u(b_k^*)$ 大于等于其他所有的$pctr_i*b_i^*$,既然其他$b_i^*$ 很配合,当然都取最小值$l(b_i^*)$ 最好,所以$u(b_k^*)$ 的条件放松到$pctr_k*u(b_k^*)$ 大于等于其他所有的$pctr_i*l(b_i^*)$,也即$u(s_k^*)$ 大于等于其他所有的$l(s_i^*)$。
证毕。
综上,$f(\cdot)$ 的单调性是算法正确性的保证,复杂度也不高,主要就是个排序。
说完1个广告位的情况,再推广到N个广告位,算法如下图,本质上是个贪心算法,先按照1个广告位的算法找出广告$k$放到广告位1,然后调整剩下广告的$u(s_i^*)\le u(s_k^*)$,不然$k$就不能保证排在第1位了,同时调整剩下广告的$u(b_i^*)$,接着在剩下的广告中按1个广告位的算法找出第2个广告位的广告,依次类推:

4. 模型校正(Calibration)
论文提到他们模型的pCVR有偏差,当真实CVR越大,pCVR和真实CVR的比值越大,也即偏差越大,所以需要校正。论文根据实验观察给出了一个校正的经验公式:
$$
p(c|u,a)=
\begin{cases}
p(c|u,a), & p(c|u,a)<tc \\
p(c|u,a)*(1+\log(\frac{p(c|u,a)}{tc})), & p(c|u,a)\ge tc \\
\end{cases}
$$
$tc$为阈值,取0.012。我们之前的做法是采用保序回归,不知道孰优孰劣。
5. 模型评估
CTR/CVR模型线下评估一般都用AUC,论文提到Google的那篇Wide & Deep Learning for Recommender Systems里表明线下AUC高上线可能效果反而变差。Wide & Deep那篇论文我之前看过,是说他们的纯Deep模型相比纯Wide模型(即LR)线下AUC降了,但线上效果反而提升了,Google作者也没给出很好的解释。
这篇阿里的论文也说他们碰到了类似的现象,于是想出一个新的指标Group AUC (GAUC),即将测试数据按照用户u和广告位p的组合(u,p)分组计算AUC(如果某个组全是正样本或全是负样本,则忽略这个组),最后再按权重求平均,权重可以是各组的展示次数或点击次数。具体公式如下:
$$
GAUC=\frac{\sum_{(u,p)}w_{(u,p)}*AUC_{(u,p)}}{\sum_{(u,p)}w_{(u,p)}}
$$
可惜论文并没详细说这么做到底能带来多少好处,是否真的解决了前面AUC线下和线上不一致的弊端。
实验结果
论文分线下模拟和线上效果做了很多角度的实验对比,这里只记录几个主要的部分。
1. 线下模拟
通过历史的log数据,将pCTR和pCVR当做真实的CTR和CVR,比如某次展示的广告计算出pCTR为4%,则认为贡献了0.04的点击。然后设计各种策略,统计关心的指标。
一共有4种策略:
- Strategy 0为对照组,保持原来线上的状态
- Strategy 1站在广告主角度,设定一个简单的调价格规则$b_a^*=b_a*(1+\sigma(\frac{p(c|u,a)}{E_u[p(c|u,a)]},w)*r_a)$
- Strategy 2就是OCPC策略,优化的目标函数前面说过,是$f(k,b_k^*)=pctr_k*b_k^**(1+\sigma(\frac{pcvr_k*v_k*||A||}{\sum_{i\in A}pcvr_i*v_i},w)*r_a)$
- Strategy 3不调出价而是直接修改rankscore公式,不再是eCPM排序,而改成按$pctr*pcvr*bid$,很明显是想提升GMV
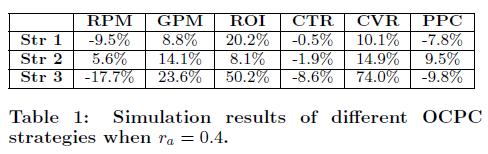
实验结果如下图,相对Strategy 0,Strategy 1和3的GPM(即千次展示GMV)和ROI都提高了但RPM降了,只有Strategy 2即OCPC策略在3个指标上都获得了提升,达到三方共赢。
2. 线上效果
Strategy 2相比Strategy 0和线下模拟一致,依然在三个指标上都获得了提升,见下图:
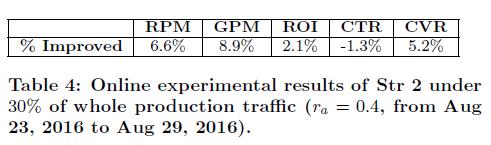
论文始终强调,这套机制具有普适性,并不局限于GMV,论文给出一个例子,双十一前淘宝商家更加关注商品加入购物篮的量,于是使用模型预测的商品加入购物篮概率pASR,修改目标函数为:
$f(k,b_k^*)=pctr_k*b_k^**(1+\sigma(\frac{pasr_k*||A||}{\sum_{i\in A}pasr_i},w)*r_a)$,
相比旧的公式,ASR指标提升15.6%。
总结
这又是一篇从实践中来的论文,针对真实场景的问题建模,算法原理也不是多么的高深复杂,却取得了很好的效果。阿里在广告主数据方面得天独厚,广告主本身就是淘宝商家,ROI的数据可以轻易获得。如果是别的广告平台想做ROI优化可能会困难重重,首先各家广告主的ROI诉求可能千差万别,其次数据共享更是难如登天。